Suites numériques et calculs

[m12]

Bonjour
Voici
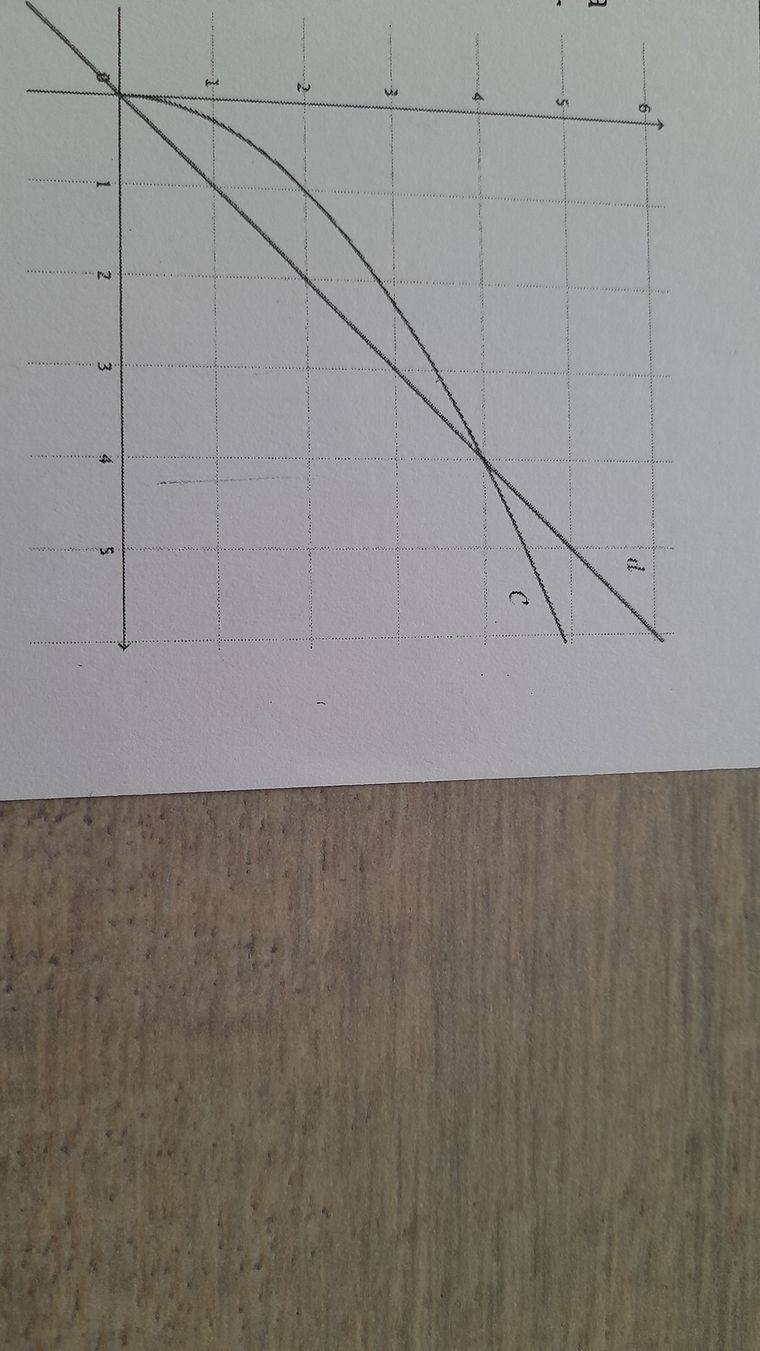
Énoncé : courbe c de la fonction f définie sur intervalle [0;+infini[ par
F(x)=2racine carre x et la droite d d equation y=x

On note U(n) la suite définie pour tout entier naturel par
U(0) =1
U(n+1 =f(U n)

1. sans calcul placer sur l axe des abscisses les 4 premiers termes de la suite

2. conjectures les sens de variation ainsi que son comportement à l infini

3)calculer les 4 premiers termes

[m12]

@m12 a dit dans Suites numériques et calculs :

Bonjour
Voici
Énoncé : courbe c de la fonction f définie sur intervalle [0;+infini[ par
F(x)=2racine carre x et la droite d d equation y=x

On note U(n) la suite définie pour tout entier naturel par
U(0) =1
U(n+1 =f(U n)

1. sans calcul placer sur l axe des abscisses les 4 premiers termes de la suite

2. conjectures les sens de variation ainsi que son comportement à l infini

3)calculer les 4 premiers termes

Pour la premières question
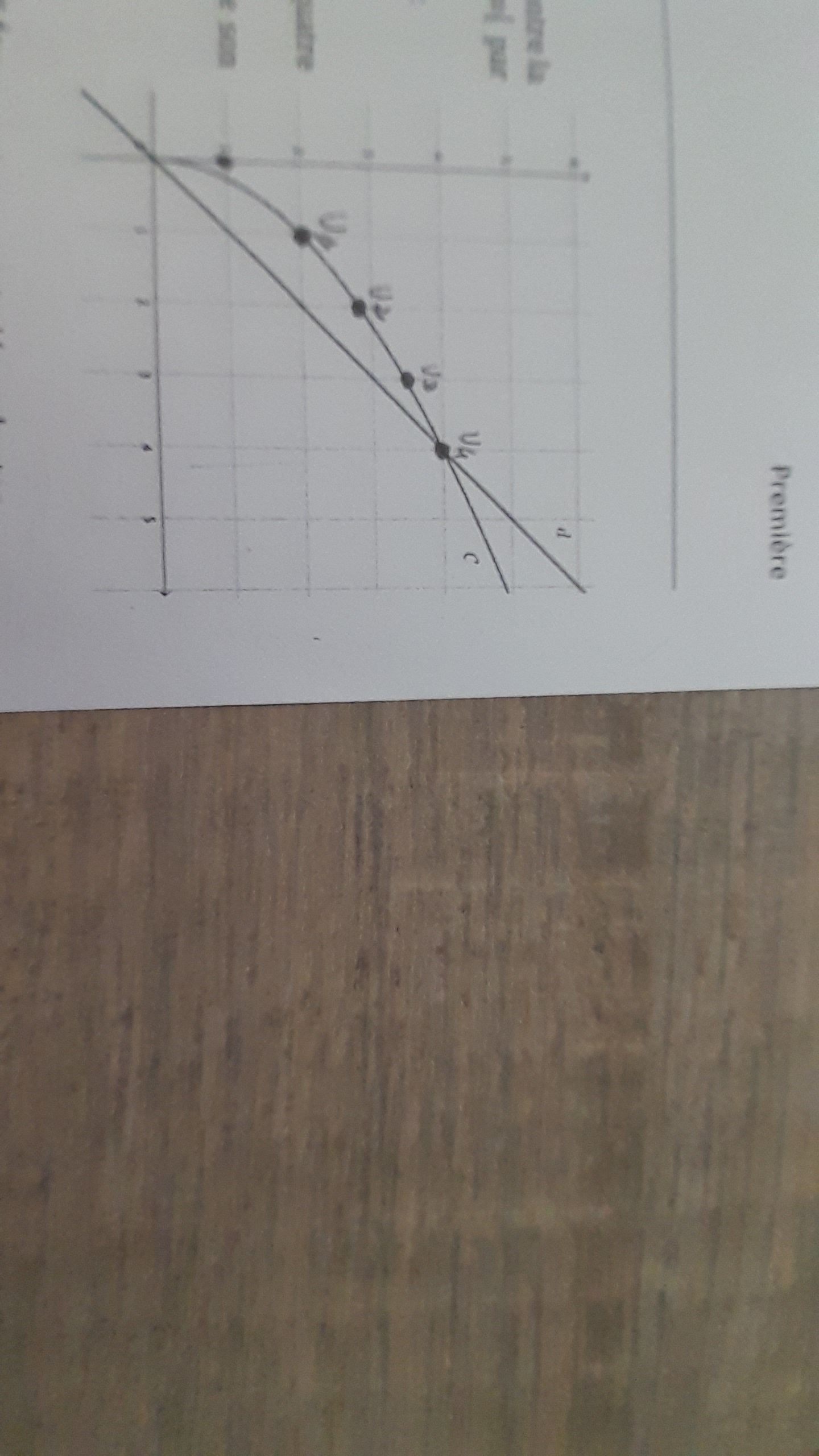
U0=1
U1=2
U2 entre 2 et 3 environ 2.8
U3 = entre 3 et 4 environ 3.4
U4=4
! )

[Noemi]

@m12 Bonsoir,

Question 1, il faut placer les quatre premiers termes sur l'axe des abscisses et non sur la courbe. Lire la valeur sur l'axe des ordonnées et la reporter sur l'axe des abscisses.

Question 3, Il faut écrire la valeur exacte.
Exemple : $u_2=f(u_1)=f(2)=2\sqrt{2}$

[m12]

@Noemi a dit dans Suites numériques et calculs :

@m12 Bonsoir,

Question 1, il faut placer les quatre premiers termes sur l'axe des abscisses et non sur la courbe. Lire la valeur sur l'axe des ordonnées et la reporter sur l'axe des abscisses.

Question 3, Il faut écrire la valeur exacte.
Exemple : $u_2=f(u_1)=f(2)=2\sqrt{2}$

Je comprends pas comment placer
C est comme cela?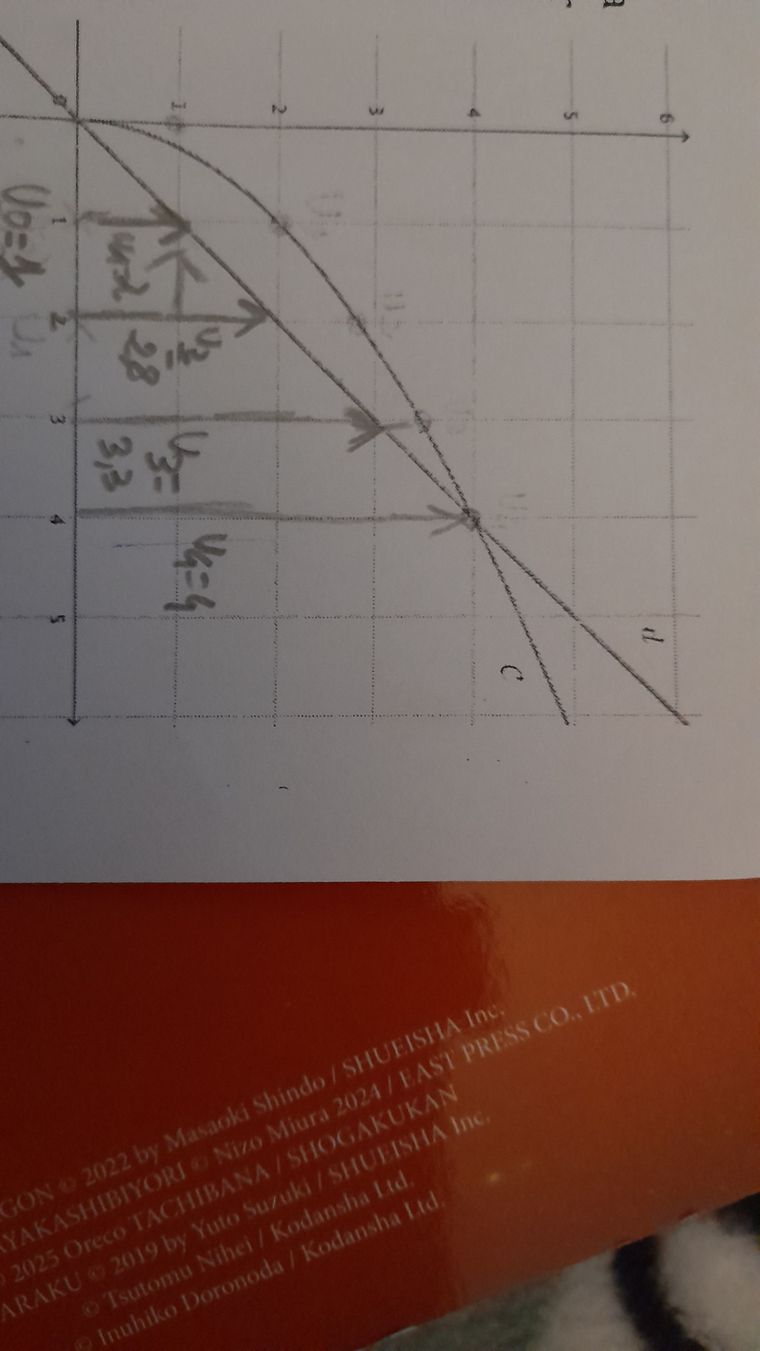

[Noemi]

@m12

$u_1$ correspond à $f(1)$, donc tu traces à partir de $x=1$ la verticale jusqu'a la représentation graphique de $f$, puis tu traces l'horizontale à partir du point d'intersection de la verticale avec la courbe. Cette horizontale coupe l'axe des ordonnées à une valeur $y_1$ qui correspond à $f(1)$ valeur que tu peux prendre sur la droite $y=x$. Tu reportes ensuite cette valeur sur l'axe des abscisses, c'est $u_1$

Tu appliques la même démarche pour les autres termes.

[m12]

@Noemi a dit dans Suites numériques et calculs :

@m12

$u_1$ correspond à $f(1)$, donc tu traces à partir de $x=1$ la verticale jusqu'a la représentation graphique de $f$, puis tu traces l'horizontale à partir du point d'intersection de la verticale avec la courbe. Cette horizontale coupe l'axe des ordonnées à une valeur $y_1$ qui correspond à $f(1)$. Tu reportes ensuite cette valeur sur l'axe des abscisses, c'est $u_1$

Tu appliques la même démarche pour les autres termes.

 

[m12]

@Noemi a dit dans Suites numériques et calculs :

@m12

$u_1$ correspond à $f(1)$, donc tu traces à partir de $x=1$ la verticale jusqu'a la représentation graphique de $f$, puis tu traces l'horizontale à partir du point d'intersection de la verticale avec la courbe. Cette horizontale coupe l'axe des ordonnées à une valeur $y_1$ qui correspond à $f(1)$. Tu reportes ensuite cette valeur sur l'axe des abscisses, c'est $u_1$

Tu appliques la même démarche pour les autres termes.

Je suis perdue
J arrive pas à visualiser

[m12]

@m12 a dit dans Suites numériques et calculs :

@Noemi a dit dans Suites numériques et calculs :

@m12

$u_1$ correspond à $f(1)$, donc tu traces à partir de $x=1$ la verticale jusqu'a la représentation graphique de $f$, puis tu traces l'horizontale à partir du point d'intersection de la verticale avec la courbe. Cette horizontale coupe l'axe des ordonnées à une valeur $y_1$ qui correspond à $f(1)$. Tu reportes ensuite cette valeur sur l'axe des abscisses, c'est $u_1$

Tu appliques la même démarche pour les autres termes.

Je suis perdue
J arrive pas à visualiser

[m12]

@m12 a dit dans Suites numériques et calculs :

@m12 a dit dans Suites numériques et calculs :

@Noemi a dit dans Suites numériques et calculs :

@m12

$u_1$ correspond à $f(1)$, donc tu traces à partir de $x=1$ la verticale jusqu'a la représentation graphique de $f$, puis tu traces l'horizontale à partir du point d'intersection de la verticale avec la courbe. Cette horizontale coupe l'axe des ordonnées à une valeur $y_1$ qui correspond à $f(1)$. Tu reportes ensuite cette valeur sur l'axe des abscisses, c'est $u_1$

Tu appliques la même démarche pour les autres termes.

Je suis perdue
J arrive pas à visualiser

C'est bon?

[Noemi]

@m12

La méthode est correcte mais le schéma est peu lisible.
Conjecture le sens de variation de la suite.

[m12]

@Noemi a dit dans Suites numériques et calculs :

@m12

La méthode est correcte mais le schéma est peu lisible.
Conjecture le sens de variation de la suite.

OK je vais le refaire mieux avec des couleurs

Pour la question 2

La suite U n est croissante car chaque terme est plus grand que le précédent

Son comportement est qu elle va vers 4 à + infini

Question 3
U1 = 2 RACINECARRE 1
= 2

U2= 2 RACINE CARRE U1
= 2 racine2
= 2.828

U3= 2 racine 2 rzcine2
=3.36

U4= 2 RZCINE 2 RACINE 2 RZCINE2
= 3.8

[Noemi]

@m12

Ecris la valeur exacte pour chaque terme de la suite puis tu précises que tu donnes une valeur approchée.

[m12]

@Noemi a dit dans Suites numériques et calculs :

@m12

Ecris la valeur exacte pour chaque terme de la suite puis tu précises que tu donnes une valeur approchée.

Donc U1 = 2
U 2= 2.824 Valeur approchée 2.8
U3= 3.3635 v à 3.4
U4= 3.6680 va 3.7

[Noemi]

@m12

Ecris les valeurs exactes avec la racine carrée.
$U_2=2\sqrt{2}$
$U_3=2\sqrt{2\sqrt{2}}$
....